Difference in py2 and py3 background models

Data Management
, ,
#1

The background model being used by pipe_tasks (I believe this is the job of meas_algorithms) apparently has gradients that are being quantified differently in python2 vs python3. The following series of images illustrates the problem and shows that the only difference is present in the background, likely due to different floating point precision.

dm-7292-screencap.png901×722 538 KB

The (row3, col3) and (row5, col3) images above have pixel value distributions that are essentially identical:

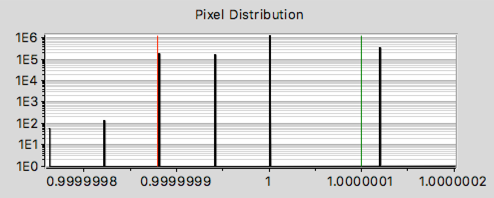
All the pixels from both
(py3_calexp + py3_bkg) / (py2_calexp + py2_bkg) and
[py3_postISR/(py3_calexp + py3_bkg)] / [py2_postISR/(py2_calexp + py2_bkg)]
are very close to 1, but differ in discrete amounts by up to ± 0.0000002. There is a discrepancy in how the background gradient is discretized between py2 and py3.

Therefore, I plan to submit DM-7292 for review with only minor formatting changes and new comments in testProcessCcd.py explaining why the thresholds (initially discussed here) are presently larger than they should be in order for the test to pass. I will open new tickets to identify and fix the underlying floating point background problem in meas_algorithms and write a test to ensure this doesn’t happen again. See: DM-8017.

2 Likes
#2

I will reiterate that there is a difference in how the background is being modeled. We haven’t tracked down the exact line of code, but I’m pretty certain it must be in something called by lsst.meas.algorithms.BackgroundSubtractionTask.

This is why we are suggesting merging pipe_tasks and then looking into meas_algorithms.

1 Like
#3

Did someone check the %pythoncode sections in the Swig .i files for integer divisions?

#4

I’m definitely thinking it might be something like that. We haven’t gone much further than this. There are a couple of integer divisions in the background subtraction task, but they don’t seem to be the problem.

#5

Because @price asked: the (py3 background - py2 background) image does differ significantly from zero. The mean = -0.00011185357 and std = 0.00035391367.