Title: Re-calibrating Photometric Redshift Probability Distributions based on Local Coverage.
Contributors: Biprateep Dey, Alex Malz, Jeff Newman, Brett Andrews
Co-signers: Johann Cohen-tanugi, Eric Gawiser, Markus Michael Rau
0. Summary Statement
This LOR pertains to a re-calibration scheme for photo-z PDFs derived by any existing estimator. PDF outputs from many photo-z methods do not follow the definition of a PDF — i.e., the fraction of times the true redshift falls between two limits z1 and z2 should be equal to the integral of the PDF between these limits for any arbitrary subset of the test data. Previous works beginning with Bordoloi+2010 have used the global distribution of Probability Integral Transform (PIT) values to re-calibrate PDFs, but offsetting inaccuracies in different regions of feature space (e.g., different ranges of colors, magnitudes, and/or fluxes) can conspire to cause the corrections derived globally to be inaccurate for large subsets of objects. We have recently leveraged a regression technique developed in Zhao+2021 that can characterize the local PIT distribution at any location in feature space in order to perform a local re-calibration of photometric redshift PDFs. We call this method Local Coverage Re-calibration (LCR) the theoretical background of which can be found in Dey+ 2021. We recommend that regardless of the photo-z algorithm chosen, local tests of PDF calibration such as the ones described in Zhao+2021 be performed and LCR or an equivalent remapping of PDFs be performed whenever the PDFs are found not to be locally calibrated. Python implementation of LCR is available publicly on Github.
1. Scientific Utility
The aim of LCR is to provide well-calibrated individual photo-z PDFs; its scientific utility will span the full range of extragalactic science from Rubin Observatory. Applications include improving localisation of transient hosts, studies of galaxy formation and evolution, AGN characterization, and those cosmological studies that exploit the individual photo-z PDFs of galaxies will benefit the most. No other comparable method exists in the literature, and so this technique has not yet been applied for existing surveys.
2. Outputs
LCR yields improved PDF estimates. The current implementation handles PDFs in a piecewise constant parameterization, but the algorithm could be modified to use any parameterization that describes the full PDF (applying the method to samples from a redshift posterior would be more difficult, however). As a free byproduct the LCR method estimates the local distribution of PIT values, allowing the identification of regions of parameter space in which redshift PDFs are particularly poorly estimated. This could be used to identify regions of feature space especially dense in catastrophic outliers.
3. Performance
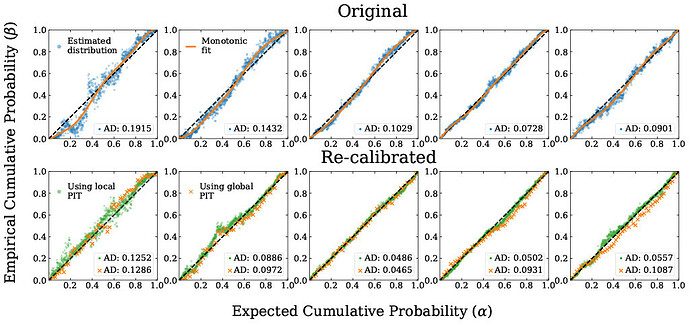
Fig.1: a) Original

b) Re-calibrated using LCR
As a proof-of-concept, we have trained the FlexZBoost [Izbicki+2017] algorithm to predict photo-z PDFs using 70% of the TEDDY A [Beck+2017 ] data set. We use the PDFs predicted by FlexZBoost for the TEDDY B and C datasets as our starting point; TEDDY B represents an independent set of objects with similar distribution in parameter space as TEDDY A, whereas TEDDY C covers a similar range of parameter space as TEDDY A but has a different distribution within that space. We use LCR to re-calibrate the PDFs using the remaining 30% of TEDDY A as our calibration set, using it to estimate the distribution of PIT values as a function of position in the feature space. Figure 1 shows the global distribution of PIT values using a P-P plot (see Schmidt+2020 for examples of how to interpret such plots in context of photo-z) for the TEDDY C data set before and after re-calibration using LCR, and quantifies the departure of the PDF of the PIT distribution from the Uniform distribution using the Anderson-Darling Statistic. We see a significant improvement in the global distribution of PIT values both visually and quantitatively, with a ~6x decrease in the value of the Anderson-Darling statistic. This demonstrates that LCR can be robust to differences in distribution between the calibration set and the objects the recalibration is applied to; more studies are pending.
The figure above shows the local distribution of PIT values before and after recalibration; We perform the re-calibration using both Bordoloi+2010’s global method and LCR. We see that our method not only improves the quality of local calibration but also outperforms Bordoloi+2010’s method for most cases.
We recommend the LCR technique be included in the Photo-Z Validation Cooperative’s evaluation process for the shortlist of estimators to be tested with commissioning data.
4. Technical Aspects
Scalability - Will probably meet. For each galaxy in the test set, LCR is locally evaluated so can be chunked up as an embarrassingly parallelizable task. The one-time training of an ML model to estimate the local distribution of PITs using a calibration set is dependent on the size of the calibration set available, but our initial tests indicate that it can be done efficiently by choosing a fast algorithm such as gradient boosted decision trees.
Inputs and Outputs - Will meet. LCR requires the input features of the PDF estimator and its output PDFs, which should already be available in the Object Catalog, though it can also accept additional features not considered by the original PDF estimator if they are available (e.g., morphology). Its outputs will also be PDFs and, optionally, a vector of corrections applied.
Storage Constraints - Will meet. The storage footprint of PDFs output from LCR is no larger than that of the input PDFs and could be smaller, though a sensitivity analysis of information loss for any particular estimator-plus-LCR has not yet been performed. In addition to the output PDFs, the calibration data and the ML model used to predict the local distribution of PIT values will need to be stored, but this should not be expensive. Preliminary tests show that good performance can be achieved by using a calibration set 2-3x smaller than the size of the data set used to train the photo-z estimator.
External Data Sets - Will probably meet. LCR requires a calibration set distinct from the training set used by the estimator. It can be a small random subset of the training data for the photo-z estimator which was hidden from the training process. Ideally, we can collect a calibration set which is much smaller than the training set but has a wider coverage of the feature space.
However, it is unlikely that the algorithm would be effective in regions of parameter space where there is no spectroscopic training data (of course, the same is true of any training-based photometric redshift method). As a result, maximizing the amount and diversity of deep spectroscopic data available for training would be valuable, for this as for all other training-based methods.
Estimator Training and Iterative Development - Will probably meet. Stress-testing of LCR to establish robustness to calibration set non-representativity is ongoing, with promising preliminary results. It is anticipated that such development will be completed prior to commissioning, though assessments of calibration set quality would continue until the calibration set is fixed.
Computational Processing Constraints - Will meet. Training a model to predict the local distribution of PIT values is the bottleneck in the whole process but preliminary tests show that a training a model on a calibration set of size 20K can be done using a single GPU based desktop in ~1min and a similar amount of time is taken for inference on a sample of size ~100K, corresponding to of order 103 compute hours to run on the full Rubin Observatory dataset. The LCR does not necessarily need GPU-based hardware and large memory nodes but their availability will certainly accelerate the inference process.
Implementation Language - Will meet. The LCR method is implemented in Python 3.