302.3 Derived Stellar Properties

Support Rubin Science Platform
#1

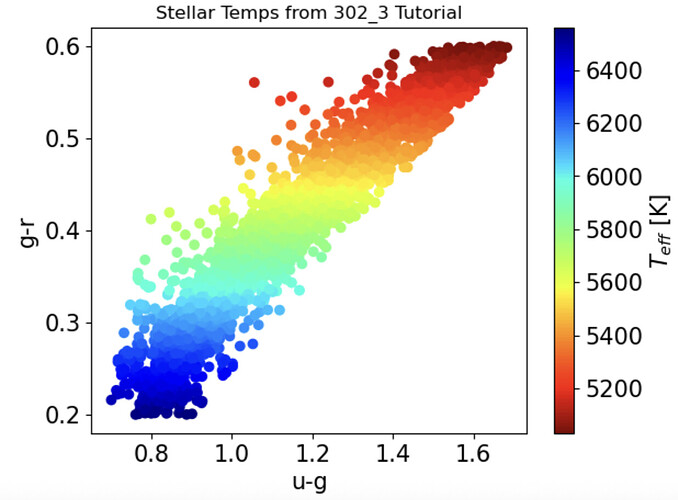
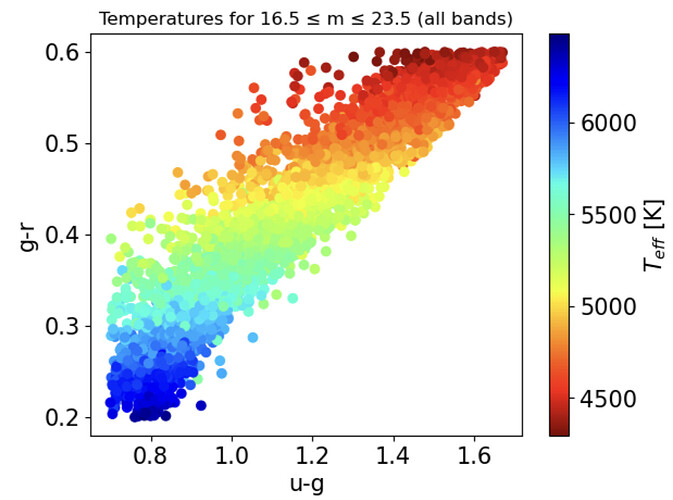
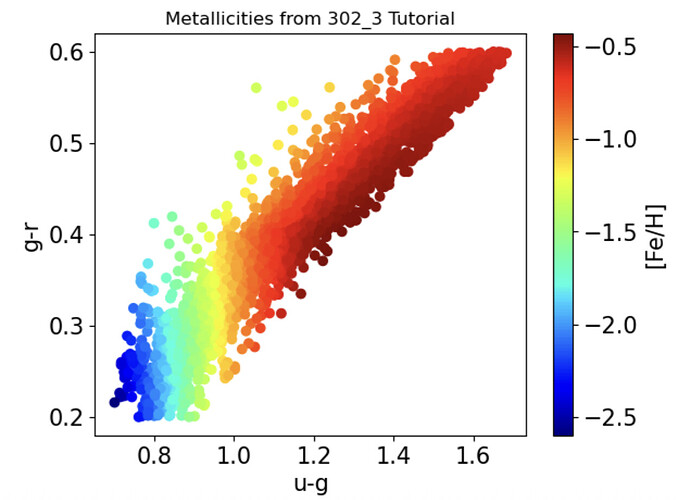
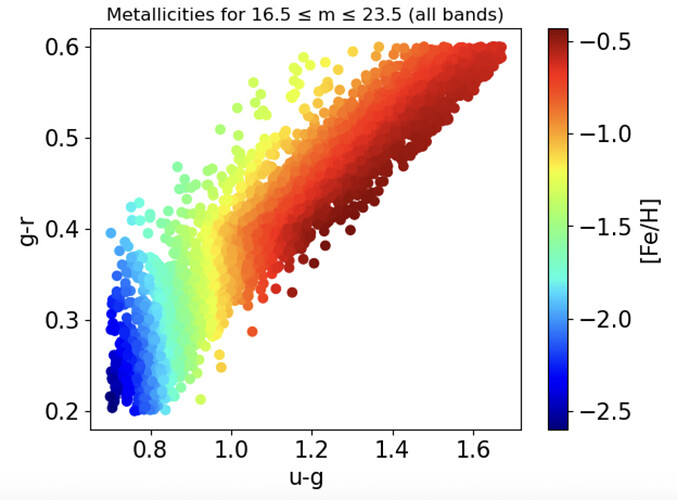
I’ve been working through RSP Notebook Tutorial 302.3 and I have suggestions and a question about this very nice tutorial.
The color transformations from ComCam to SDSS are based on RTN-099 (this document has many, many other transformations in it as well). I think the boundary conditions should be included with the transformations so, instead of:

ug = objtab["u_psfMag0"] - objtab["g_psfMag0"]
gr = objtab["g_psfMag0"] - objtab["r_psfMag0"]
gi = objtab["g_psfMag0"] - objtab["i_psfMag0"]
ri = objtab["r_psfMag0"] - objtab["i_psfMag0"]
iz = objtab["i_psfMag0"] - objtab["z_psfMag0"]

gi_sdss = 1.065*gi + 0.005
gr_sdss = 1.058*gr + 0.058*ri - 0.002
u_sdss = objtab["u_psfMag0"] + 0.587*gi**2 + 1.424*gi + 0.758 where -1.1 < gi_sdss <= -.4
u_sdss = objtab["u_psfMag0"] + 0.063*gi**2 - 0.192*gi + 0.263 where -0.4 < gi_sdss <= 0.8
u_sdss = objtab["u_psfMag0"] - 0.0003*gi**2 + 0.174*gi + 0.059 where 0.8 < gi_sdss <= 3.9

may I suggest:

ug = objtab["u_psfMag0"] - objtab["g_psfMag0"]
gr = objtab["g_psfMag0"] - objtab["r_psfMag0"]
gi = objtab["g_psfMag0"] - objtab["i_psfMag0"]
ri = objtab["r_psfMag0"] - objtab["i_psfMag0"]
iz = objtab["i_psfMag0"] - objtab["z_psfMag0"]

gi_conditions = [(gi > 0.2) & (gi <= 3.1)]
gi_outputs = [(1.065*gi + 0.005)]
gi_sdss = np.select(gi_conditions, gi_outputs, default=np.nan)

gr_outputs = [(1.058*gi + 0.058*ri -0.0020)]
gr_sdss = np.select(gi_conditions, gr_outputs, default=np.nan)

# Set the conditions for gi_sdss
u_conditions = [
    (gi_sdss > -1.1) & (gi_sdss <= -0.4),
    (gi_sdss > -0.4) & (gi_sdss <= 0.8),
    (gi_sdss > 0.8) & (gi_sdss <= 3.9)
]

# Define the outputs based on those conditions
u_outputs = [
    objtab["u_psfMag0"] + 0.587 * gi_sdss ** 2 + 1.424 * gi_sdss + 0.758,
    objtab["u_psfMag0"] + 0.063 * gi_sdss ** 2 - 0.192 * gi_sdss + 0.263,
    objtab["u_psfMag0"] - 0.0003 * gi_sdss ** 2 + 0.174 * gi_sdss + 0.059
]

# Apply the conditions
objtab['u_sdss'] = np.select(u_conditions, u_outputs, default=np.nan)

Also, I used 16.5 ≤ m ≤ 23.5 instead of the SDSS range of 14 < m < 19.5. The results for all these changes produce little change in the temperature and metallicity plots, other than to add more data points.

Do those modifications make sense?

My last question is about the transformation of g-r from ComCam to SDSS:

gr_sdss = 1.058*gr + 0.058*ri - 0.002

The relation is not explicitly given in RTN-099 (did I mention what a great document that is?) and I haven’t been able to replicate it. I’ve tried g_sdss - r_sdss and (g-i)_sdss - r_sdss + i_sdss. Could my math be bad?
Thank you again for all these tutorials : )

#2

Thank you, @babel for your suggestions and questions! We’ve created an internal ticket to implement your suggestion to the tutorial.

Regarding the question about modifying the SDSS magnitude range, while I haven’t tested this specific scenario personally, I would recommend caution. Applying these relationships to stars outside the calibrated range may require additional validation to ensure accuracy.