Heliocentric coordinate system definitions in DP0.3

Support Data Preview 0
, ,
#1

Hi all, hope this message finds you well! I am new to the Rubin community forum, hope I am posting this in the right place – if not, please let me know, and I’d be happy to re-post somewhere else :slight_smile:

I am a master’s student at Marshall University working on Solar System anomaly detection / SETI research with Rubin for my thesis, using the DP03 dataset. The TL;DR version of my question is: where could I find out how the heliocentric coordinates are defined in the DP0.3 Solar System simulation? (e.g. for heliocentricVX, heliocentricVY, etc., from the SSSource Table). I am just curious how the x,y,z axes are defined relative to the other orbital elements in the simulation, if that makes sense. I hadn’t come across a definition like this in the Data Product Definition Document or elsewhere so thought I would ask – apologies if I have overlooked this in the documentation somewhere!

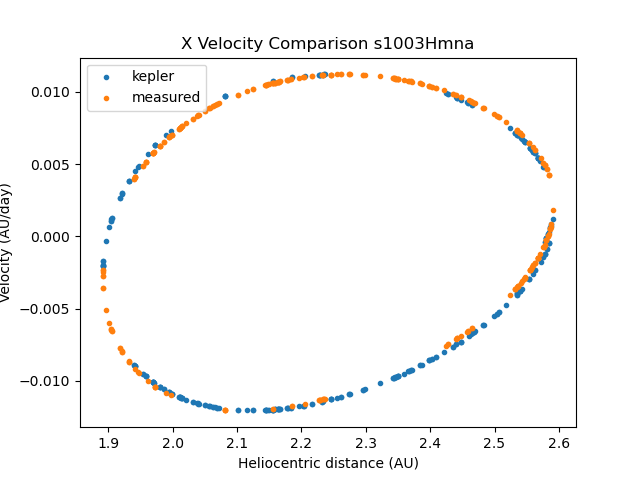
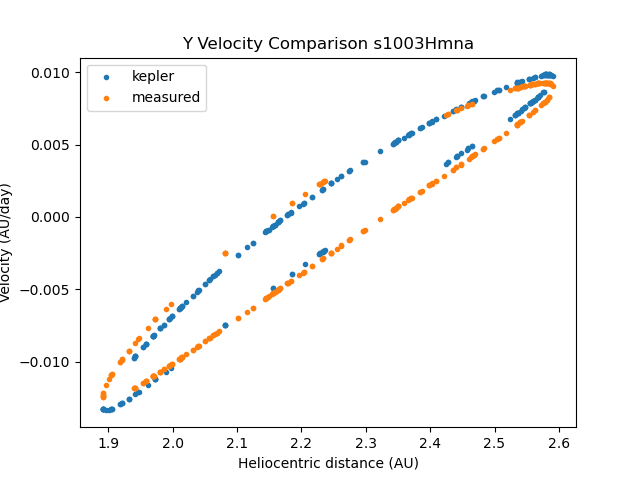
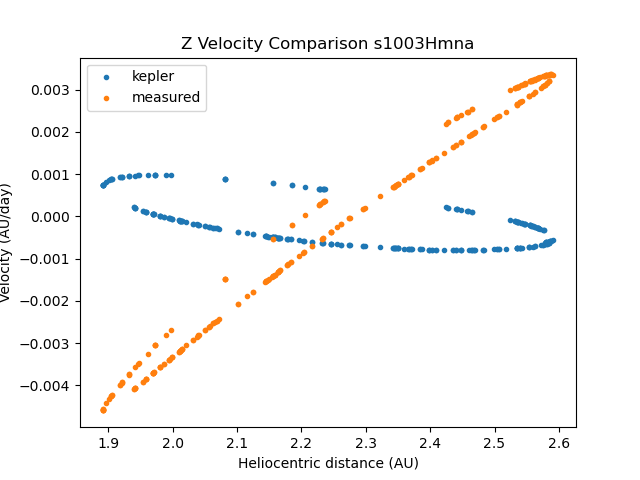
Here is the longer version: Currently, I am working on comparing the predicted (Keplerian) velocities of objects in the simulation (calculated using Kepler’s equations and the orbital elements from the simulation) with the “measured” heliocentric velocities (i.e., heliocentricVX, heliocentricVY, etc.), in an attempt to detect objects that display non-gravitational acceleration. Through my calculations (which I have performed using poliastro and independently verified with code that I wrote to perform the same function), I have found that the heliocentricVX and heliocentricVY velocities agree well with the Keplerian predictions for a few example objects, but there are large discrepancies between heliocentricVZ and the predicted Keplerian Z velocities. I am wondering if the coordinate system definition that I am using is different from that used in DP03, and if so, if that could be causing the discrepancies I am seeing. I have attached some sample plots at the bottom of the post for reference.

If there is anything about the above explanation that I can clarify or provide further information about, please let me know and I would be happy to do so! Thank you so much for your time and consideration!

xvelocity_s1003Hmna
yvelocity_s1003Hmna
zvelocity_s1003Hmna

#2

Hi Ellie, thanks for posting this. I don’t think you’ve overlooked anything in the documentation, the only definition I can find is in the DP0.3 schema, e.g., “Cartesian heliocentric Z velocity (at the emit time)”. I also wonder if the coordinate systems might be different - but then it’s a bit odd that only the Z axis is affected? The Rubin team will follow up, but also it might be helpful if you have a code snippet of the calculations you did with poliastro, how the Kepler Z velocity in the final frame was calculated.

In the meantime, anyone else with insight here is most welcome to chime in…

#3

Hi Melissa, thank you so much for your reply and for looking into this! Yes, I can absolutely share a code snippet – I did the calculations in two different ways. First I tried programming the calculations independently, then compared those results with poliastro’s and found that the results agreed exactly. Here is code that I wrote to do the same calculations as poliastro:

def keplerian_velocity_xyz(r, a, e, i, node, peri, x, y, df): 

    # r = heliocentric distance (~ distance from 1 focus)
    # a = semi-major axis
    # e = eccentricity
    # n = mean daily motion
    # i = inclination
    
    # n = mean motion
    # mean motion is the average angular distance traveled per day
    n = np.sqrt(G_au_d / (a**3))
    
    ## true anomaly
    nu = df.apply(return_nu, axis=1)
    
    sin_E = (np.sin(nu) * np.sqrt(1 - e**2)) / (1 + e * np.cos(nu)) 
    cos_E = (e + np.cos(nu)) / (1 + e * np.cos(nu)) 
    E = np.arctan2(sin_E, cos_E) 
    
    ## unrotated coordinates and vector
    X_dot = (-(a*n*np.sin(E))/(1-e*np.cos(E)))
    Y_dot = ((a*n*np.sqrt(1-(e**2))*np.cos(E))/(1-(e*np.cos(E))))
    
    v_XYZ = [X_dot, Y_dot, 0]

    ## rotation matrix
    P11 = np.cos(node)*np.cos(peri)-np.sin(node)*np.cos(i)*np.sin(peri)
    P12 = -np.cos(node)*np.sin(peri)-np.sin(node)*np.cos(i)*np.cos(peri)
    P13 = np.sin(node)*np.sin(i)
    
    P21 = np.sin(node)*np.cos(peri)+np.cos(node)*np.cos(i)*np.sin(peri)
    P22 = -np.sin(node)*np.sin(peri)+np.cos(node)*np.cos(i)*np.cos(peri)
    P23 = -np.cos(node)*np.sin(i)
    
    P31 = np.sin(i)*np.sin(peri)
    P32 = np.sin(i)*np.cos(peri)
    P33 = np.cos(i)
    
    P = np.array([[P11, P12, P13], [P21, P22, P23], [P31, P32, P33]])
    
    # need to replace this with numpy dot product...    
    v_xyz = [P11*v_XYZ[0]+P12*v_XYZ[1]+P13*v_XYZ[2], P21*v_XYZ[0]+P22*v_XYZ[1]+P23*v_XYZ[2], P31*v_XYZ[0]+P32*v_XYZ[1]+P33*v_XYZ[2]]
    
    x_dot = v_xyz[0] #X_dot #v_xyz[0] #X_dot #
    y_dot = v_xyz[1] #Y_dot*np.cos(i) #v_xyz[1] #Y_dot #
    z_dot = v_xyz[2] #-Y_dot*np.sin(i) #v_xyz[2]
    
    return x_dot, y_dot, z_dot

## here is the function I used to compute the true anomaly: 
def return_nu(row):
    #return np.arccos(row['heliocentricX']/row['heliocentricDist']) + ((1.5*np.pi) if row['heliocentricY'] < 0 else 0)
    
    node = row['node'] * np.pi/180 
    peri = row['peri'] * np.pi/180 ## argument of the perihelion
    i = row['incl']* np.pi/180
    
    P11 = np.cos(node)*np.cos(peri)-np.sin(node)*np.cos(i)*np.sin(peri)
    P21 = np.sin(node)*np.cos(peri)+np.cos(node)*np.cos(i)*np.sin(peri)
    P31 = np.sin(i)*np.sin(peri)
    
    x = row['heliocentricX']
    y = row['heliocentricY']
    z = row['heliocentricZ']
    
    X = P11*x + P21*y + P31*z
    
    if row['heliocentricY'] < 0:
        return (2*np.pi) - np.arccos(X/row['heliocentricDist'])
        
    else: 
        return np.arccos(X/row['heliocentricDist'])

Note that I used the equations provided on pages 16 and 18 of Klioner’s Lecture Notes on Celestial Mechanics: https://arxiv.org/pdf/1609.00915

The poliastro version of the code (which achieves the same results) is not as explicit since the calculations are hidden in the function calls, however if you’d like to check out that code, it is linked here (lines 98~122): lsst_seti/sycorax_search/prep_csv.py at main · ewhite42/lsst_seti · GitHub

The source code for poliastro is available here if you’d like to dig into their code as well: poliastro/src/poliastro at main · poliastro/poliastro · GitHub

If there is anything about the above that I can clarify, please let me know and I’d be happy to do so :slight_smile: Again, many thanks for looking into this!

#4

Hi

Could this be confusion between heliocentric ecliptic and heliocentric equatorial coordinates?

JJ

#5

Thanks for your reply! That is a good question – poliastro has a feature that allows you to choose whether to use the ecliptic or equatorial plane as your reference, and I tried both options and obtained similar results, with the z velocities still showing the same differences. However I am wondering a bit if the feature was actually enabled given the fact that the results that it gave for both ecliptic and equatorial planes were so alike – not sure if that is to be expected, or if that sounds off to you? I can go back and plot the version with “equatorial” selected overlaid with the data with “ecliptic” selected each other and send that along if that would be of interest!

#6

See DP0.3 lacks solar elongation angle data? - #12 by jrob93

#7

Thank you so much, Meg – this is exactly the issue we are having! That is really helpful to know. Really appreciate your help getting this sorted out! :slight_smile:

#8

Hi @ewhite42 - I wanted to briefly follow-up to say that we’ve now identified a bug with the HeliocentricZ and HeliocentricVZ values in the DP0.3 SSSource table that is likely due to a missed coordinate system conversion. The bug has now been added to the “Known Issues” listed in the DP0.3 documentation, which can be found here: The DP0.3 Simulation — Rubin Observatory DP0.3.

1 Like
#9

Thank you so much, @sgreenstreet, for the super helpful follow up! Great to see the updates to the documentation as well :slight_smile: Really appreciate the information!!